“The child who receives a hammer for Christmas will discover that everything needs pounding.”
One of my friends asked about “Six Sigma,” famously used by General Electric and Motorola to enhance the quality on their production lines, and famously used by Home Depot and 3M for short term gain and long term failure, (see “Six Sigma, So Yesterday,” on Business Week OnLine, here).
“I understand that Six Sigma means a very high quality system – with only 3.4 errors per million units,” my friend said. “What I don’t understand,” he added, “is the definition in terms of Standard Deviation and Normal Distribution. 99.99966% of the values will fall within 6 Standard Deviations of the Mean, compared to 99.73% of the values falling within 3 Standard Deviations of the Mean. What’s a standard deviation? And what’s a normal distribution?”
Before I get to the good stuff – the numbers – consider that “Six Sigma” is a tool. Jerry Weinberg in “The Secrets of Consulting,” (Dorset 1986, ISBN: 978-093-263301-9 / blog) explains “The Law of the Hammer.” “The child who receives a hammer for Christmas will discover that everything needs pounding.” When people find a tool that works very well some of the time they may begin to believe that it works terrifically well all of the time. Six Sigma is such a tool. It may work very well some of the time – on assembly lines and in logistics. But it is not applicable in all situations, and clearly not well suited for areas where creativity and customer service drive value.
This may explain the failures of Six Sigma by Robert Nardelli at Home Depot, James McNerney at 3M, and Anne Fudge at Young & Rubicam. Nardelli, McNerney and Fudge were GE alumni. I imagine that they understood Six Sigma. What they appear not to have understood is that a given tool, no matter how useful in some situations, is not useful in other situations.
Now, on to the numbers –
The first thing to remember is that the Greek letter Sigma, σ, is used by statisticians to represent “Standard Deviation.” This of course, raises the question, “What’s a standard deviation?”
Sigma, σ, or Standard Deviation, measures whether the data are clustered around the mean or spread out, and how tightly clustered or how widespread.
“Six Sigma,” sometimes written as 6σ, means “Six Standard Deviations,” or more technically, “within six standard deviations above and below the mean.” As noted above, 99.99966% of the data within a data set are within six standard deviations from the mean. Standard Deviation, Variance, to which it is related (Standard Deviation is the square root of the Variance) and other statistical values are properties of sets of data. They are meaningful when evaluating large sets of data – thousands, hundreds of thousands, millions of data points, or more.
(Since Standard Deviation is the square root of Variance, the next questions are”What is Variance?” and “How do we calculate Variance?” Glad you asked. Variance is defined as the average of the squared differences of each data point from the mean. You get it by adding up the values of the data points and dividing the sum by the number of items, to find the arithmetic Mean. Then you square the difference of each data point and mean, add these values together, divide by number of data points, and that’s the Variance. Take the square root of the Variance, and you have the Standard Deviation. A lower Variance and Standard Deviation means the data are clustered together. Higher Variance and Standard Deviation means the data are spread out. (see Math Is Fun ) That may be interesting, but it’s not germane to the topic of Standard Deviation in terms of Six Sigma as a measure of quality.
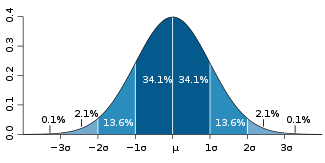
What is relevant is that Standard Deviation measures the variation from the Mean. Most data sets in the real world are “Normally Distributed, that is, they form bell shaped curves, as pictured above. Most of the data are clustered around the arithmetic mean, with 68.25% of the data falling within one Standard Deviation, 95.46% within two, 99.73% within three, and 99.99966% within six Standard deviations, six sigmas.
In plain English, this means that in any given a production run, with quality to 3.0 sigma, then 99.73% will be acceptable, but 0.27 will be defective. If you raise the quality to Six Sigma, then 99.99966% will be acceptable and only 0.00034% will be defective. A 3 Sigma run of 1.0 million widgets will have 2,700 defects. A Six Sigma run of 1.0 million widgets will have 3.4 defects. If the cost per defect is $500, then the defect related cost of 3 Sigma production is $1.35 million. (This is 2,700 defects multiplied by $500.) The cost of defects at Six Sigma is only $200. If the cost of moving to Six Sigma is $1.0 Million, then the cost of defects at Six Sigma is $1,000,200 – and the enterprise saves money by going to Six Sigma. The savings are greater with larger production runs or with higher costs of defects.
As noted above, GE is the most famous successful Six Sigma company. 3M and Home Depot, however, were spectacular failures. Six Sigma did not save them money. In fact it cost them. Where efficiency works on an assembly line and in logistics, it doesn’t work in a product development environment or a service environment.according to Bolman and Deal, in “Reframing Organizations: Artistry, Choice, and Leadership,” (C 2008, Jossey Bass, ISBN 978-0-7879-8799-2),
“In the short run, McNerney’s strategy paid off. Indicators of productivity improved, costs were trimmed, and the stock price soared. But Six Sigma’s standardization began to intrude on 3M’s historical emphasis on innovation. Prior to McNerney’s Arrival [from GE] new ideas were accorded almost unlimited time and funding to get started. Fifteen percent of employees’ on the clock time was devoted to developing groundbreaking products – with little accountability. This approach had given birth to legendary products like Scotch Tape and Post-It Notes.
“Six Sigma systematized the research and development process. Sketchy, blue-sky projects gave way to scheduled, incremental development. Funds carried an expiration date, and progress thru a planned pipeline was measured and charted. Development of new products began to wane. “The more you hardwire a company on total quality management, [the more] it is going to hurt breakthrough innovation,” says Vijay Govinarajan, a management professor at Dartmouth.”
If manufacturing process can be made more efficient by looking at events within the Six Sigma, then emergency preparedness we need to focus on outliers – events beyond the Six Sigma. Events like Hurricanes Katrina and Irene, like the Deepwater Horizon disaster in the Gulf of Mexico of April to July 2010, and the Kingston, Tennessee coal ash spill of December, 2008, like the Earthquake / Tsunami system that hit Japan and triggered melt-downs at three of the nuclear reactors at Fukushima Dai-Ichi.
Disclosures:
Neither Mr. Nardelli, Mr. McNerney, nor Ms. Fudge were contacted prior to publication. However, they are welcome to contact me.
I am not long on any of the companies mentioned in this post, but I think GE and 3M are interesting. I like CEO Jeff Immelt’s focus on “EcoImagination,” and I shop at Home Depot. Mr. Immelt was also not contacted for this blog post, but is welcome to contact me.
Reframing Organizations, Artistry, Choice, and Leadership, by Lee G. Bolman and Terrence E. Deal, is required reading for the Marlboro MBA in Managing for Sustainability. It’s a great book, and a great MBA program. While I contacted Lee Bolman on an unrelated matter back in 2009 after reading his book, I did not contact him or Terrence Deal for this blog post. They are, of course, welcome to contact me.
Jerry Weinberg‘s”The Secrets of Consulting,“is not required reading for the the Marlboro MBA in Managing for Sustainability. However, I heartily recommend it. However, I did not contact Jerry Weinberg for this blog post. He is, of course, welcome to contact me.